Step 1: Input of Dipolar Splittings

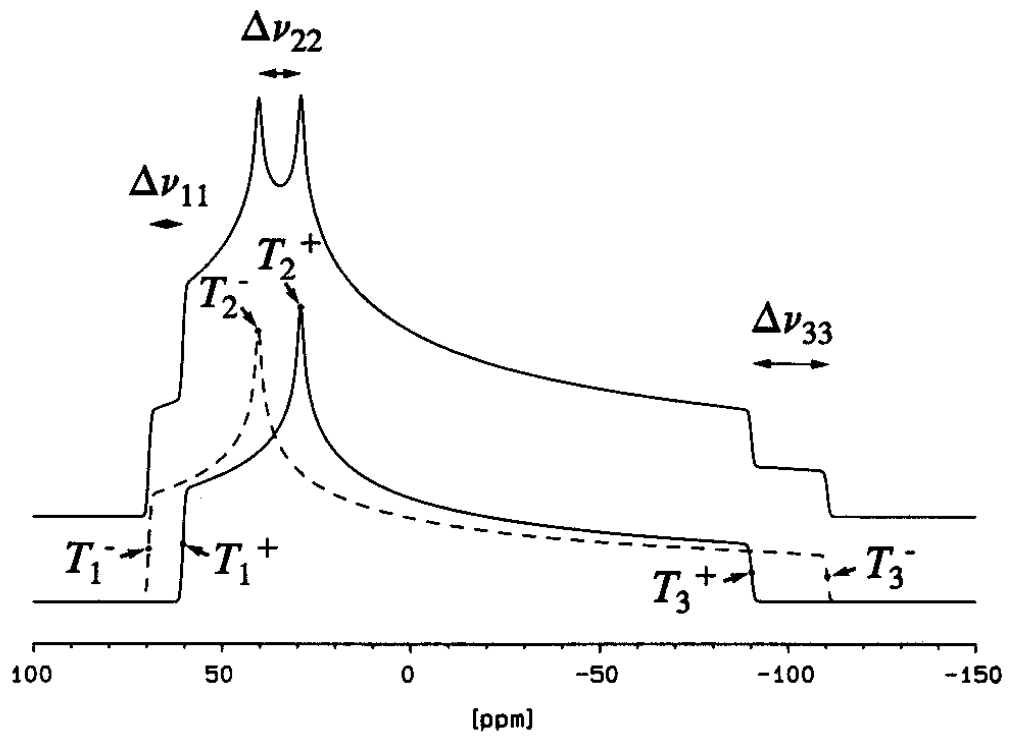
THE DIPOLAR SPLITTINGS:

• If the chemical shift interaction is the dominant interaction, the magnitude of the splittings Δν_ii at δ_ii can be calculated from:
  Δν₁₁ = R_eff (3 cos² α sin² β - 1)
  Δν₂₂ = R_eff (3 sin² α sin² β - 1)
  Δν₃₃ = R_eff (3 cos² β - 1)
  R_eff is the effective dipolar coupling constant, β is the angle between the most shielded principal component, δ₃₃, and the internuclear vector, while α is the angle between the least shielded component, δ₁₁, and the projection of the internuclear vector on the δ₁₁,δ₂₂ plane. Because the dipolar interaction is traceless, only two of the splittings Δν_ii are independent.
• In order to find all possible mutual orientations which are consistent with the observed splittings, three ratios of the dipolar splittings are calculated. These ratios as functions of α and β are represented in a triangular plot generated by this program. For each absolute value of a ratio, two contour lines of opposite sign exist. Generally, six different contour lines will be created by this program. However, three of them will overlap each other. Your first step in the analysis is to identify this unique curve!
• The dipolar splitting ratio method requires the input of the dipolar splittings (in Hz) about the principal components of the chemical shift tensor (δ₁₁, δ₂₂, δ₃₃), as observed in the experimental spectrum (δ₁₁ corresponds to the component at highest frequency).